简单题,题目大意是给定两个数 \(a\) 、 \(b\) ,求 \(x\) 、 \(y\) 使得 \(gcd(x, y) = a\) , \(lcm(x, y) = b\) ,问由多少对这样的 \((x, y)\) ,其中 \(gcd(x, y)\) 为 \(x\) 、 \(y\) 的最大公约数, \(lcm(x, y)\) 为 \(x\) 、 \(y\) 的最小公倍数。解题思路主要利用 \(x \times y = gcd(x, y) \times lcm(x, y)\) 就行了。WA 了两次是因为没看清楚题意 "x and y, one line for each test.",太马虎了。代码如下:
#include <stdio.h>
#include <math.h>
long gcd(long a,long b) {
return b ? gcd(b, a % b) : a;
}
long lcm(long a, long b) {
return a / gcd(a, b) * b;
}
int main(int argc, char *argv[]) {
long a, b;
long m;
int sum;
while(scanf("%ld%ld", &a, &b) != EOF) {
if (a == b) {
sum = 1;
}
else {
m = a * b;
sum = 0;
int i;
for (i = 1; i < sqrt(m); ++i) {
if (((m % i) == 0) && (gcd(i, m/i) == a)) {
sum += 1;
}
}
sum *= 2;
}
printf ("%d\n",sum);
}
return 0;
}顺便,用了两个月的 FVWM-Crystal,感觉虽然轻量,但是有些细节颇有不便之处,比如每次新开窗口的时候窗口的大小和位置都“不太确定”——就是有时候窗口会覆盖底下的 panel、有时候整个窗口又比整个屏幕都大……恰逢前天晚上兴奋无眠,因此便邪恶的敲了下面一条命令:
编译过程比较顺利,又陆续装了 GDM, GNOME Do 等小工具,配上 Mac4Lin 的主题,现在整个桌面看起来还是蛮 pp 的:
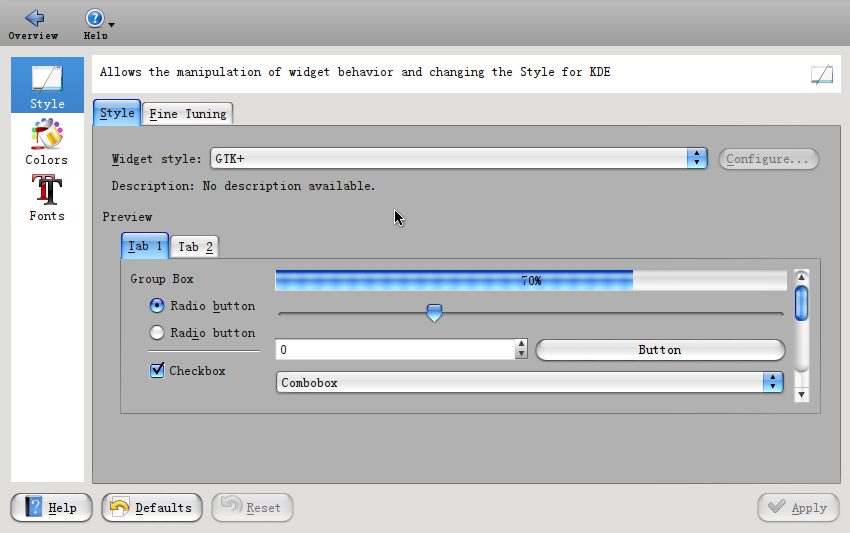
还有一个小问题就是 GTK+ 和 Qt 程序风格二异。我的解决方案是安装 KDE 的 control center
然后在 widget style 中选择 GTK+ 风格,如下图所示:
效果还算不错。其余的解决方案可以参考:
就是这样。嘿。